Diffusion Imaging
Making important discoveries from diffusion imaging studies requires images to be of high SNR and geometric accuracy. Achieve those improvements and gain access to new acquisition methods with field monitoring.
The use of diffusion imaging in both fundamental neuroscience and translational research is increasing. Diffusion imaging allows for detailed visualization of in vivo microstructure and function neuronal tracts. Alterations in some diffusion parameters have even been shown to be reliable as predictive biomarkers for disease state.
Reproducibly acquiring high quality, geometrically accurate diffusion images is technically challenging. The diffusion encoding and readout processes can lead to significant artifacts which distort the image. Susceptibility and eddy current artifacts are common examples of how the image can become geometrically distorted during the encoding and readout process. Various sequence adaptations have been developed to mitigate these artefacts. For example, multi-shot phase-encoded segmented EPI reduces effective echo spacing, reducing the influence of static susceptibility-related artefacts at the cost of increase sensitivity to nuisance image phase. Double spin-echo diffusion preparation is an example of a sequence change to reduce the sensitivity of the image to eddy-current distortions, at the cost of an increased image echo time, and commensurate image SNR penalty.
Repeatable techniques in diffusion imaging should minimize scan to scan variability caused by scanner or off-target subject influences (breathing, cardiac function). Doing so allows for changes in brain physiology to more reliably be quantitated, potentially with greater statistical power. The reliability of repeated scans on the same scanner, between scanners at the same site, and across multiple sites has become it’s own area of research, with emphasis put on finding diffusion acquisition and processing methods that improve reproducibility and provide potential lower bounds for reliable measurements.
However, in order to be repeatable, diffusion data must be geometrically accurate and of high SNR. Both SNR and geometric accuracy are a function of how well an image is encoded. Image encoding is the process by which the scanner localizes and acquires signal. Many factors influence the quality of image encoding, including gradient performance and magnetic field fluctuations during the scan.
Image geometry is important any time the physical dimensions or locations of structures are being analyzed or when images are being registered to other sequences or modalities. Image geometry is also highly susceptible to distortions caused by magnetic field fluctuations. Diffusion encoding gradients stretch and skew images, leading to different geometry for each diffusion direction.
Geometric accuracy in diffusion images can be restored using field monitoring. Field monitoring captures field fluctuations due to eddy currents from gradient encoding lobes. Image reconstruction using these data removes the distorting effect of the gradients.
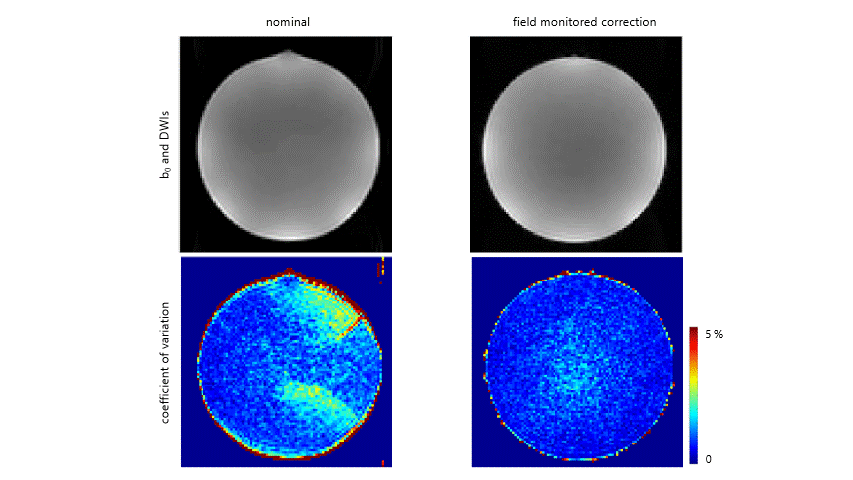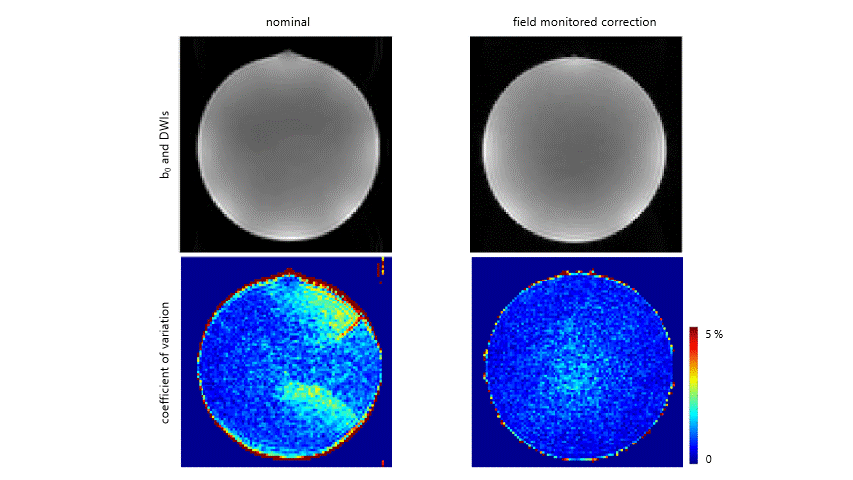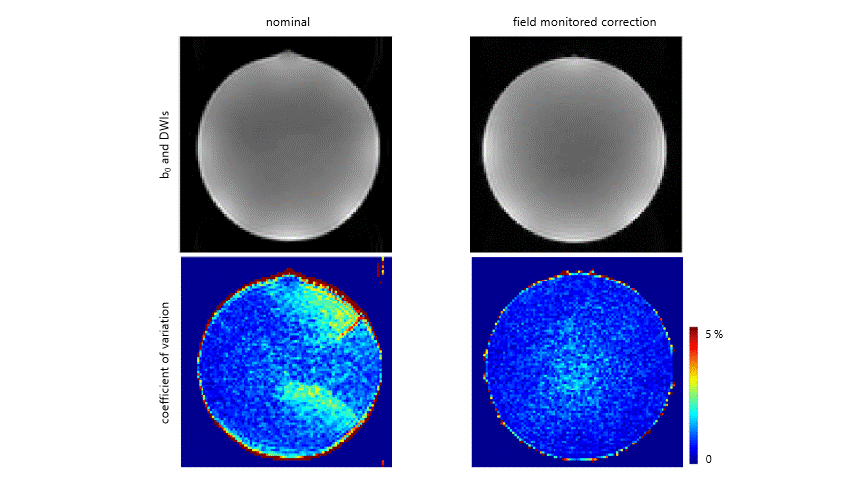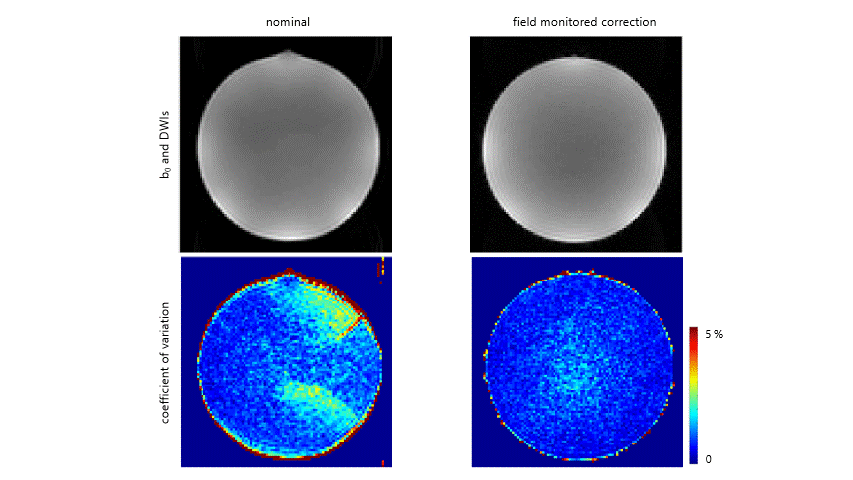
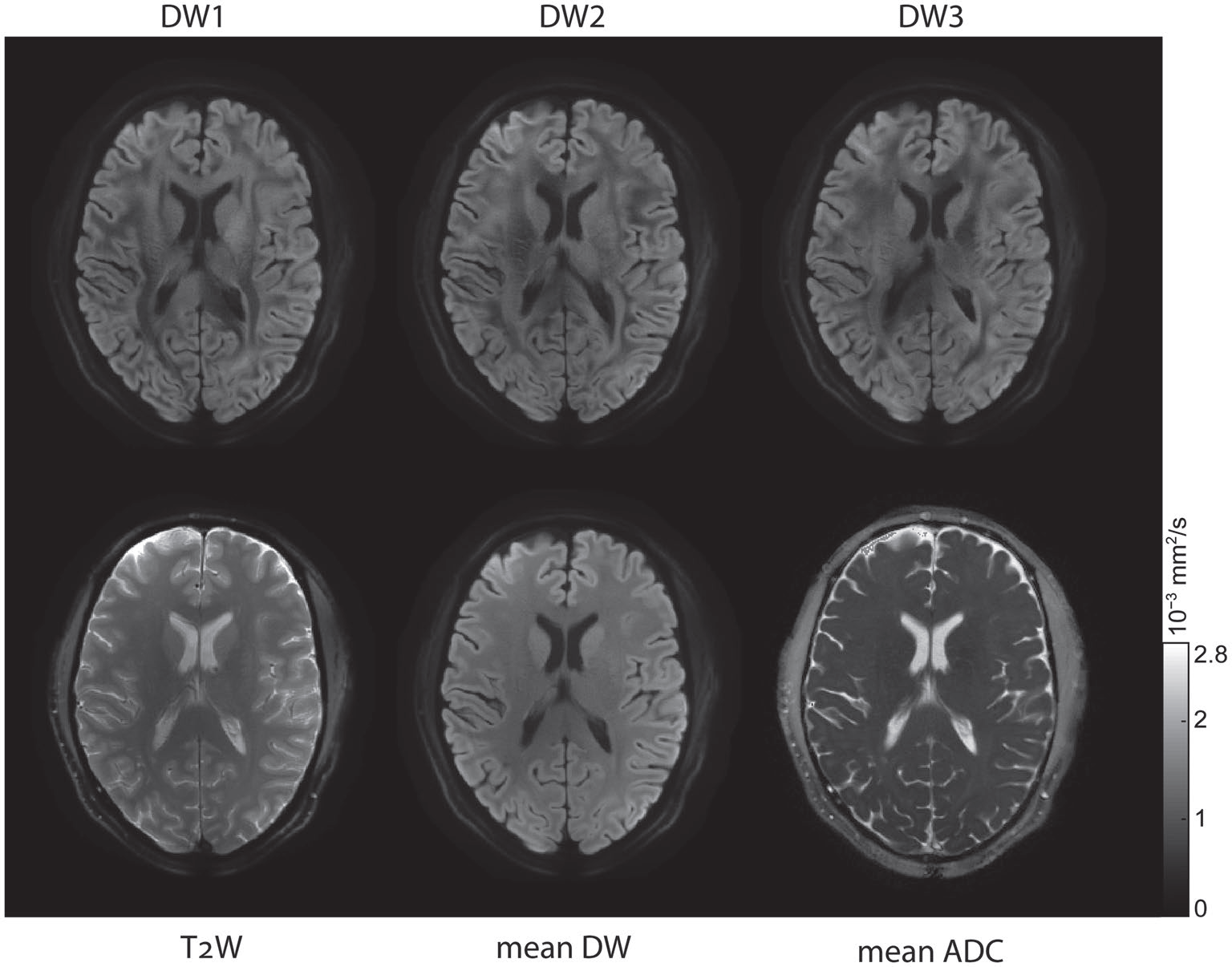
Ma et al. demonstrated the need for eddy current removal from Human Connectome Data using the Clip-on Camera to monitor in vivo scans. Dr. Ma’s results demonstrate the HCP style sequences suffer from eddy currents generated by diffusion encoding gradients and that the images can be reconstructed without such distortions when the eddy currents are measured, improving image quality.
Advances in diffusion imaging aim to optimize acquisition for image SNR, resolution, total acquisition time, and robustness to subject motion. Improving these image characteristics makes smaller lesions or structures more visible and contrast differences between structures more reliable. Improvements aim to increase the reproducibility of derived parameters (i.e. ADC) and potentially improve the statistical power of analyses.
Implementations which aim to improve SNR aim to reduce the effect of T2* decay during image readout by reducing the echo time of the image, and acquiring the MR signal before it has dephased away. Spiral readouts acquire images starting at the center of k-space and can therefore have significantly shorter TEs than EPI readouts. Spiral readouts also have the advantage of being more robust to subject motion.

Lee et al. demonstrated the benefits of spiral readouts for diffusion imaging on a standard clinical 3T scanner. Their results demonstrate that spiral acquisitions had higher SNR than all of the EPI methods tested (image shows their spiral implementation versus the traditional Stejskal-Tanner and twice refocused spin echo EPI implementations).
Wilm et al. developed an implementation of spiral diffusion using a high slew rate (up to 1200 T/m/s) gradient set (see also Hennel, et al.). The high slew rate allows k-space to be traversed more quickly during the imaging readout, allowing one to sample all of the relevant portions of acquisition space before the signal has decayed away. This speed can be used to acquire a standard resolution image in less time than could be done with a full body gradient set or to acquire higher spatial resolution with usable SNR.
These results are also impactful in that they calculated the acquired k-space traversal up to 5th order spherical harmonics. This helped to account for the more spatial complex field evolution of their gradient. They did this using the Dynamic Field Camera positioned in multiple locations in the bore and combining the data in a “virtual probe” manner to fit to higher order basis functions. In the image below from Wilm, 2020 (see link below), we can see how a principal component analysis of the spatiotemporal phase evolution due to eddy currents looks for this particular spiral read-out module.
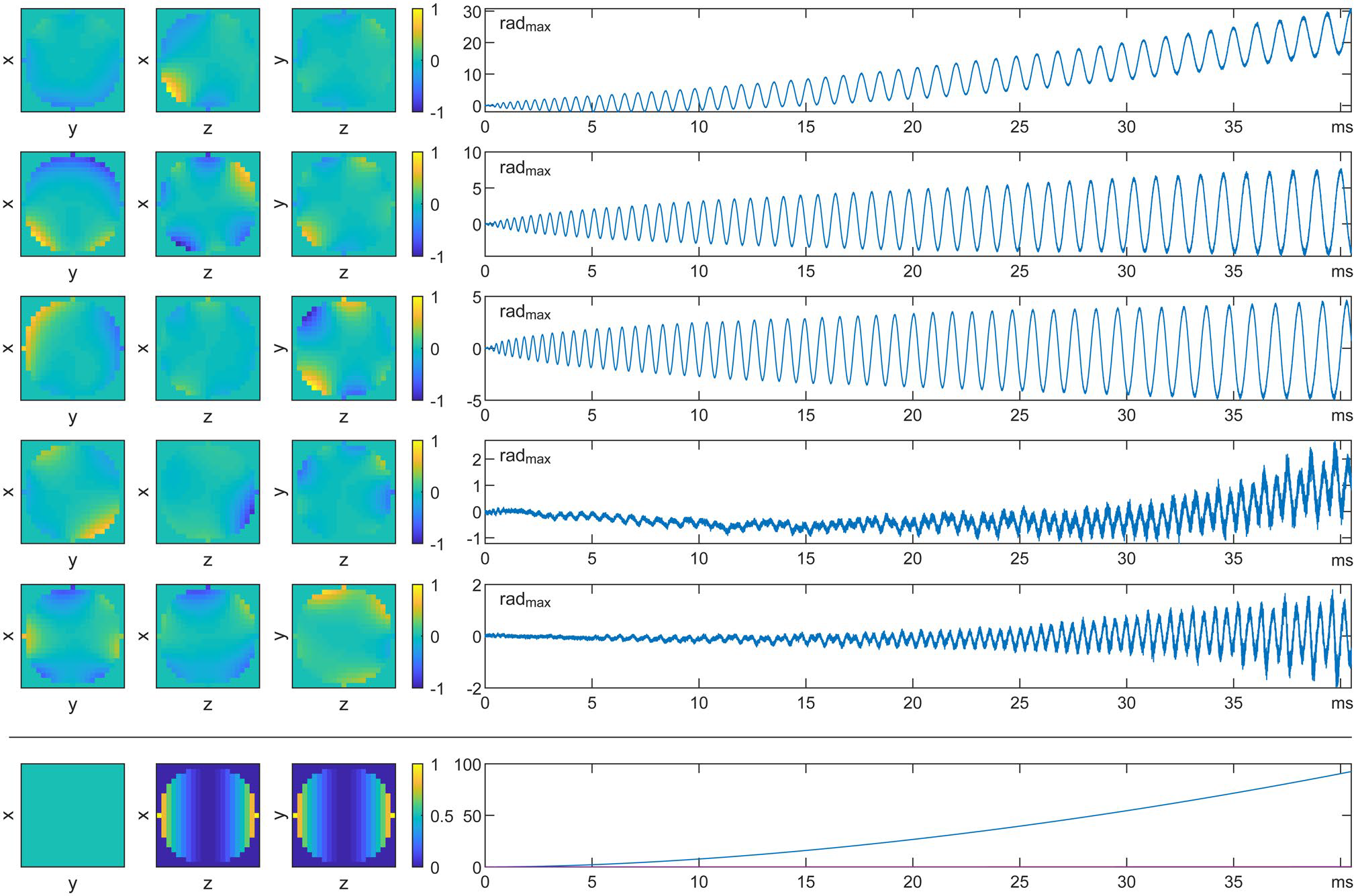
Properly accounting for this extra phase in the image reconstruction (Wilm et al., 2016) allows for the high quality diffusion images to be recovered from the measured data.